(Re)learning how to use VoiceOver
I was rereading I Used The Web For A Day Using A Screen Reader and realized that it's been a while since I last used VoiceOver (the built-in screen reader for Mac) to proof the content of my posts and pages.
I said "fine, let's fire it up and listen to what the page I was reading sounds like". It wasn't as easy as I thought as I've forgotten most of the commands that I used to navigate content with Voiceover.
So, rather than have to commit this to memory I'll post it here and generate a PDF of the post later.
Getting started #
If you haven't used VoiceOver before I highly recommend that you run the VoiceOver tutorial. To get there follow these steps:
Go into System Preferences.
Click on Accessibility. You will see the accessibility preferences shown below.

macOS Big Sur Accessibility preferences main dialogue
Click on VoiceOver. You will see the VoiceOver preferences shown below. There are two buttons, the one on the left will open VoiceOver Training and the one on the right will open the VoiceOver Utility.

macOS Big Sur Voice Over accessibility preferences
We'll revisit the utility later in the post.
The shortcut for turning VoiceOver on and off: ⌘ + F5 (⌘ is also known as the Cmd key).
Is VoiceOver speaking too fast? Open VoiceOver Utility hit the ‘Speech’ tab, and adjust the rate accordingly.
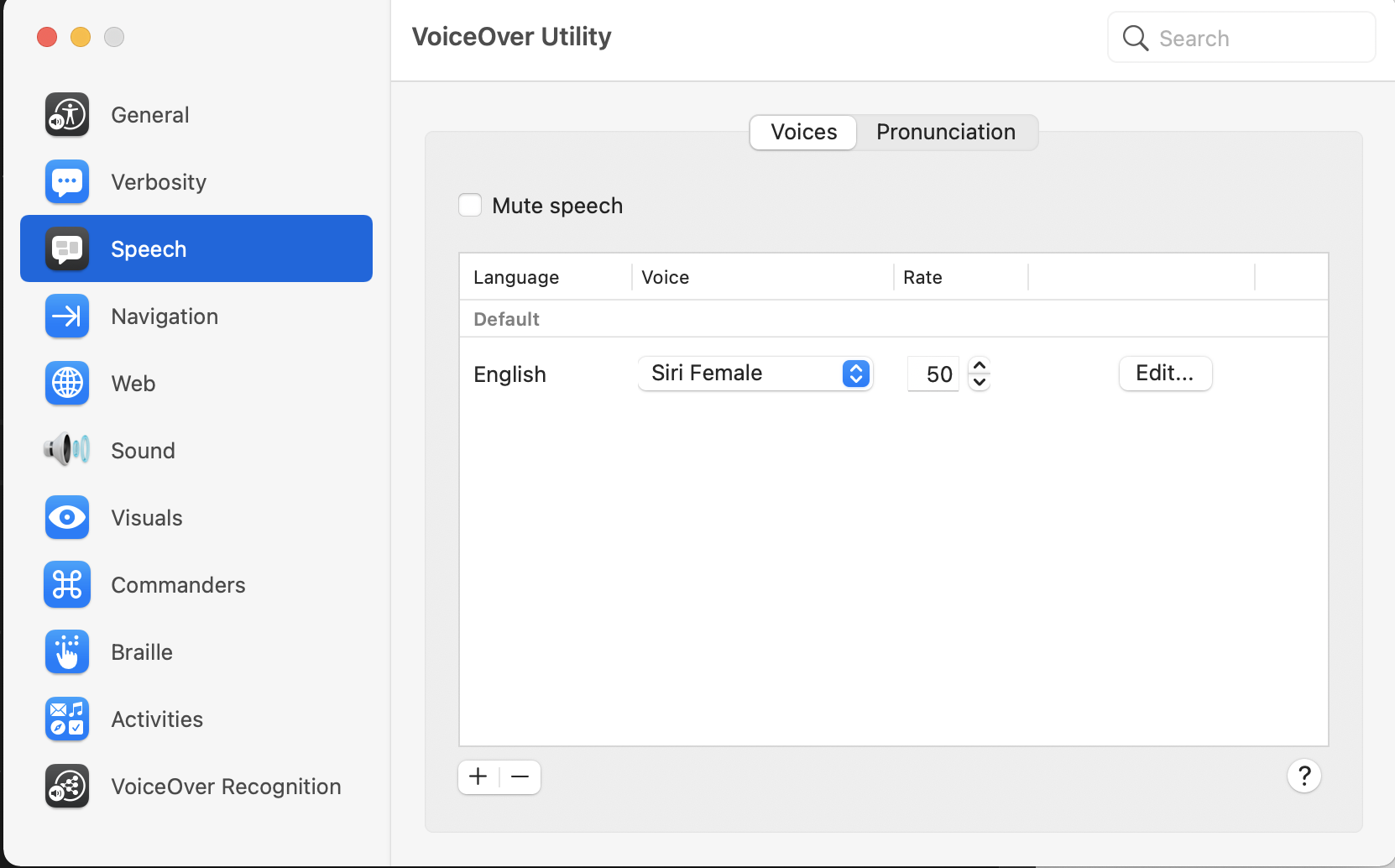
VoiceOver Speech settings that allow you to control the voice used and the speed of the spoken description
Once you’ve mastered turning it on and off, you’ll need to learn to use the “VoiceOver key” (which is actually two keys pressed at the same time): Ctrl and ⌥ + M (the ⌥ key is also known as “Option” or the Alt key). Using the VO key in combination with other keys, you can navigate the web.
help when you don't remember #
There are times when you know the name of the command but you can't remember the key combinations you need to run, you can use the VoiceOver Commands Help.

A screenshot of the Commands Help menu. A panel with a black background and white text, titled Commands Help. The menu includes these items, from top to bottom: General, Information, Navigation, Text, Web, Find, Tables, Size and Position, Audio, Braille, Visuals, Hot spots, Jump. To the right of each item is an arrow to access an item’s submenu.
To find a VoiceOver command:
-
When VoiceOver is on, open the Commands menu by pressing VO H H
-
Type some letters of the command name to narrow the Commands menu to just those commands that contain the letters you typed.
- Use the arrow keys to navigate the Commands menu until you hear the command you want. To list all commands again, press Delete.
-
When you hear the command you want to use, press the Return key or the Space bar to apply the command to the item in the VoiceOver cursor.
Navigating through content #
You can use VO + A to read the web page from the current position. If you have the VO mapped to it's default keystroke combination this means holding Ctrl + ⌥ + A.
You may use VO and arrow keys (VO + → and VO + ←) to go through each element in the DOM in sequence. When you come across a link, you can use VO + Space to click it — you’ll use these keys to interact with form elements too.
Heading and Landmark Navigation #
As a sighted users, we seldom, if ever, read every word on a web page, we usually ‘scan’ pages for interesting information as fast as possible.
Screen reader users have use content type navigation to achieve the same reading speed.
One way to navigate by content type is to open the shortcuts menu with VO + U, navigate to the content type you want with the ← and → arrow keys, then navigate through those elements with the ↑↓ keys.
Conclusion and next steps #
This is a very basic introduction to VoiceOver. There's a lot more you can do as a user of screen readers and as a developer building content that screen readers will interact with.
In addition to being a good introduction to using VoiceOver I Used The Web For A Day Using A Screen Reader presents examples of accessing sites with VoiceOver and techniques to fix accessibility issues revealed during the site's visit.
The W3C keeps a comprehensive list of specifications, guidelines, and techniques under the Web Accessibility Initiative umbrella.
Of particular interest, to me, are: How to Meet WCAG (Quick Reference) for developers and an Introduction to Web Accessibility for designers.
Finally, for users in the United States, it is important to point out that:
The 2018 Section 508 refresh requires most federal websites to meet or exceed the guidelines laid out for Level AA compliance testing with WCAG 2.0. Source: What Is Section 508 Compliance?
